Fusion Propulsion

Fusion propulsion is a potential future mode of propulsion for travel from Earth to Mars, or other destinations.

General Physical Characteristics of Fusion Propulsion Systems

Fusion rockets use a propellant, which in most systems is comprised of the reaction products, unspent fuel, and other material directly involved in the underlying fusion reaction. These materials are contained within a reaction chamber and ejected via a magnetic nozzle. The nozzle typically includes an energy recovery system that is used to power the ignition system, called the ‘‘driver’’. A secondary energy production system is usually required to enable start-up of the propulsion system.

In some variations, the driver may be powered by an external source.

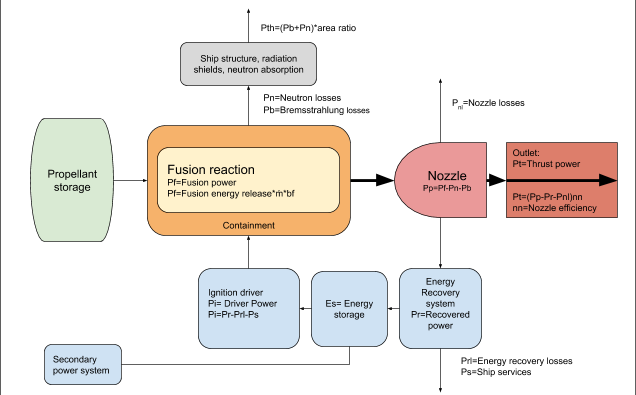
The power flow within a fusion propulsion system is shown in the following graph. The graph also shows the physical systems that are required to produce fusion propulsion system.

This diagram shows a flowchart for a fusion drive

Fusion drive example

Pf= Fusion power, Pf=Fe*ṁ*bf
Pp= Plasma power, Pp=Pf-Pn-Pb
Pn= Neutron losse s
Pb= Bremsstrahlung losses
Pt= Thrust power, Pt=(Pp-Pr-Pnl)*ηn
Pnl= Nozzle (reaction chamber) power losses
Pr= Recovered power, Pr=Prl-Ps
Prl= Energy recovery system power losses
Ps= Power to ship services
Pi= Driver power (ignition power)
Es= Energy stored in energy recovery system
Pth= Thermal power loads from radiation losses, Pth=(Pn+Pb)*area ratio
ηn= Nozzle efficiency
bf= Burnup fraction
ṁ= Mass flow of propellant
G= Gain, G=Pf/Pi
Fusion power = fusion energy release*mass flow*burnup fraction, Pf=Ef*ṁ*bf
Plasma power = Fusion power-Neutron losses-bremsstrahlung losses, Pp=(Pf-Pn-Pb)ηn
Thrust power = (Plasma power-Recovered power-Nozzle power losses)*nozzle efficiency, Pt=(Pp-Pr-Pnl)ηn
Ignition power = Power recovery-Power recovery system losses- Ship services, Pi=Pr-Prl-Ps

Recovered power may be replaced by an external source. Project Longshot() used a separate nuclear reactor to power ignition.

Fusion gain = Fusion power/ Recovered power, G=Pf / Pr

According to Newton’s laws of motion the vehicle thrust (F) is equal to the mass flow rate (ṁ) times the exhaust velocity(ve) and the efficiency of the nozzle (ηn):

F=ṁ*ve*ηn

Since for a rocket the power (P) can be related to the thrust by the following equation: Pt=1/2ṁve2 or

ve =√(2Pt/ṁ)

It follows that the thrust is related to the power by:

F=ṁ*√(2Pt/ṁ)*ηn or
F=√(ṁ*2Pt)*ηn

The rocket equation uses the exhaust velocity Ve to find the mass ratio of the vehicle and the final rocket velocity:

Rocket equation:

Vf=Ve*ln(mo/mf)

If the mass flow is constant (as per most of these fusion designs) the distance crossed while under power is:

s=Ve*(t-(m0/ṁ))*ln(m0/mf)+t(Vo-Ve)

where (t) is the time under power and Vo the initial velocity.

Using a mass flow (ṁ) of 1 kg/s and power (P) of 35 300 GW, and supposing an overall efficiency of 0,8, including fusion losses, the thrust from a fusion drive will be F=√(1kg/s*35300GW*2)*0,8= 8 403 000 N or 857 tonnes. This is about ¼ of the thrust of the Saturn 5 rocket. And a power level much greater than the entire energy production of present human civilization. As can be seen, the mass flow of fusion products will be very low for lower powers. Therefore it is unlikely that fusion could be use for launching from planetary surfaces, but would be more appropriate for interplanetary travel.

Pure fusion is rather overpowered for Mars transportation. Fusion is more interesting when additional propellant is added to the drive, the power is reduced and the thrust increased.

Aneutronic reactions

This is discussed further below, but ideally we would like reactions which do not produce neutrons. These are hard to turn into viable thrust, and when they hit the metals of the rocket they can damage the crystal structure and weaken the metal. There are some fusion reactions that do not produce neutrons, but they tend to be harder to initiate fusion.

Possible fusion reactions

D+T(Deuterium + Tritium) fusion is the easiest to ignite, though it ejects a high-energy (14.1 MeV) neutron that holds most of the energy and poses problems for engine design. Moreover, Tritium has a very short half-life, 13.5 years, so it radioactive and decays into He3. D+T works fine for Earth or Mars based power reactors, which is why it is used for most of the present research projects on fusion, and since the high energy neutron can combine with lithium to produce a new tritium atom, a D+T reactor can ‘breed’ its own fuel.

D+He3(Deuterium+Helium3) fusion is often favored as a space vehicle fuel because it is intrinsically aneutronic. However, any DHe3 mixture produces unavoidable DD(Deuterium+Deuterium) reactions as well, and at a higher rate in some temperature ranges(). The DD side-reactions produce their own neutrons, plus Tritium, which reacts immediately with available deuterium in the plasma to produce the aforementioned 14.1 MeV high energy neutrons. This all significantly limits the nominal aneutronic benefit. In addition, He3 is almost completely nonexistent on Earth or Mars, with most supplied from tritium decay, and is incredibly scarce in the potential resources of remote places like the Moon and the gas giants(3). Reactors producing He3 as byproducts would be useful. He3 might be produced on Earth using D-D breeder reactors. These could feed higher power D+He3 reactors, and in particular D+He3 engines for space vehicles that would require less shielding than equivalent D+D or D+Tritium engines.

D+D fusion is an interesting option since Deuterium is readily available via seawater separation, distillation and hydrogen isotope separation on Earth or on Mars, and can be stored cryogenically indefinitely, given an appropriate refrigeration system. It also isn’t radioactive when compared to Tritium. Its major downside is that there are two equally probable DD fusion reactions, one that produces Tritium and a proton, and one that produces He3 and a high energy neutron. The Tritium, with it’s lower fusion temperature, will fuse and create the 14.1 MeV neutron already mentioned. The waste energy of the high energy neutrons cannot be recaptured easily, but some drive designs manage to do it. The D+D mix is harder to ignite than D+T, but easier than D+He3. The cascade fusion of 6 Deuterium atoms (table 1, reaction 11) produces 2 He4 atoms, 2 protons and 2 neutrons. About 40% of the energy release is carried by the neutrons.

p+B11 is another interesting reaction that does not produce any neutrons. And it has the further benefit that there are no secondary reactions, as opposed to D-He3 mixes. It is very difficult to initiate, however, and may lose excessive amounts of energy through electromagnetic (bremstalhung) radiation for a drive. It is actively studied()() as a power source, however. Bremstralhung radiation might be recovered using x-ray tuned photocells. It’s also important to note that releases about a quarter of the energy per kg of other reactions, so a Boron powered spaceship might require more propellant, depending on the burnup fraction.

Fusion Propulsion may be used for Mars transfer in the future, once the technology is functional. Mars has a higher amount of deuterium in its water than Earth, so this basic fusion fuel might be easier to obtain on Mars.

Significant fusion reactions that could be used for a fusion engine
Reaction				→	Products									Total Energy release	Atomic mass of products
						ratio	MeV/ fusion			MeV/ fusion			MeV/ fusion	GJ/kg	N
1	D	+	T	→	He4	100%	3.49	+	n0	14.1				340 000	5
2a	D	+	D	→	He3	50%	0.82	+	n0	2.45				79 000	4
2b		+	D	→	T	50%	01.01	+	p+	03.02				97 000	4
3	D	+	He3	→	He4	100%	3.6	+	p+	14.7				353 000	5
4	T	+	T	→	He4	100%		+	2x n0				11.3	182 000	6
5	He3	+	He3	→	He4	100%		+	2x p+				12.9	207 000	6
6a	He3	+	T	→	He4			+	n+	12.1	+	p+		195 000	6
6b		+	T	→	He4		4.8	+	D	9.5				230 000	6
6c		+	T	→	He4		0.5	+	n0	1.9	+	p+	11.9	230 000	6
7a	D	+	Li6	→	He4			+	He4				22.4	270 000	8
7b		+	Li6	→	He3			+	He4		+	n0	2.56	31 000	8
7c		+	Li6	→	Li7			+	p+				5.0	60 000	8
7d		+	Li6	→	Be7			+	n0				3.4	41 000	8
8	p+	+	Li6	→	He4		1.7	+	He3	2.3				55 000	7
9	n	+	Li6	→	He4			+	T	2.3					7
10	He3	+	Li6	→	He4			+	He4		+	p+	16.9	181 000	9
11	p+	+	B11	→	3x He4								8.7	70 000	12
12	6D			→	2x He4		8.92	+	2n0	16.55	+	2p+	17.72	348 000	12
Total energy release = sum of energies (MeV) x 1.6e-19 J/eV / mass of reaction products Mass of reaction products = N x atomic mass unit (1.66e-27 kg) In a fusion reaction, the portion of the fuel that actually reacts is called the burnup fraction. As a first order of magnitude evaluation, we can establish that a fusion drive with a burnup fraction of 10%, using 1 kg of deuterium+he3 per second will produce 353 000 GJ/kg x 1kg/s x 0,1 = 35 300 GW of power (Line 4, table 1). To find the thrust from the fusion reaction, F=ṁ2Ptηn . For an efficiency (ηn) of 80%, the force is 5 600 KN or 576 tonnes. To find the exhaust velocity Ve=F/ṁ= 56 500 000 N / 1 kg/s = 5 650 000 m/s