Difference between revisions of "Hohmann transfer"
m (Minor hyperlink correction) |
m (Minor syntax edits) |
||
| Line 1: | Line 1: | ||
{{Stefan}} | {{Stefan}} | ||
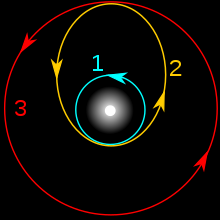
[[File:Hohmann_transfer.gif|thumb|right|400px|Animated depiction of Hohmann transfer]] | [[File:Hohmann_transfer.gif|thumb|right|400px|Animated depiction of Hohmann transfer]] | ||
| − | In orbital mechanics, a Hohmann transfer describes the path taken to transit between two orbits of differing radii while traveling 180° around their common focus. Conventional analyses consider such a path to be the most efficient transfer method for traveling between | + | In orbital mechanics, a Hohmann transfer describes the path taken to transit between two orbits of differing radii while traveling 180° around their common focus. Conventional analyses consider such a path to be the most efficient transfer method for traveling between circular orbits located on the same plane.<ref name=":0">Let’s Go to Mars! Calculating Launch Windows Activity. (n.d.). Retrieved July 5, 2019, from NASA/JPL Edu website: <nowiki>https://www.jpl.nasa.gov/edu/teach/activity/lets-go-to-mars-calculating-launch-windows/</nowiki></ref><ref name=":1">[2] Basics of Space Flight - Solar System Exploration: NASA Science. (n.d.). Retrieved July 5, 2019, from NASA Solar System Exploration website: <nowiki>https://solarsystem.nasa.gov/basics/chapter4-1/</nowiki></ref><ref name=":2">Hohmann Transfer Orbit & Total Travel Time. (2001). Retrieved July 5, 2019, from <nowiki>http://www.polaris.iastate.edu/EveningStar/Unit6/unit6_sub2.htm</nowiki></ref> |
==Description== | ==Description== | ||
| Line 24: | Line 24: | ||
===Type-I and Type-II Trajectories=== | ===Type-I and Type-II Trajectories=== | ||
[[File:TypeIandIItrajectories.png|right|250px|thumb|Potential Earth-Mars alternatives to the Hohmann transfer (represented by the thick, black semicircle). The green dotted line represents a trajectory which leaves sooner, traveling beyond the target orbit before encountering it on its second intercept. The red dashed line leaves and arrives later on its first intercept.<ref name=":4" />]] | [[File:TypeIandIItrajectories.png|right|250px|thumb|Potential Earth-Mars alternatives to the Hohmann transfer (represented by the thick, black semicircle). The green dotted line represents a trajectory which leaves sooner, traveling beyond the target orbit before encountering it on its second intercept. The red dashed line leaves and arrives later on its first intercept.<ref name=":4" />]] | ||
| − | As discussed above, the Hohmann transfer involves a trajectory carrying the spacecraft precisely 180° around the Sun. This method requires the lowest expenditure of energy, but does come with the disadvantages of extended travel time and launch window limitations. These disadvantages can be compensated for to a certain degree by increasing fuel expenditure and altering the time of departure. The resultant trajectories will arrive at the target after proceeding less than 180° around the Sun (Type-I Trajectory) or more than 180° (Type-II).<ref name=":1" /> Both trajectory types carry the spacecraft beyond the target orbit and therefore cross it two times—by timing the arrival of the target with one of these two intersections, the spacecraft can still reach its destination, allowing more flexibility in terms of launch times and/or transit duration. These advantages come at the cost of increased energy expenditure: not only does the spacecraft have to accelerate more at the departure point, it also must spend extra fuel decelerating at the destination in order to match the target orbit<ref name=":2" /><ref name=":4" />. For a trip from Earth to Mars, decreasing travel time by 10% necessitates twice as much fuel, while cutting travel time in half requires ten times as much; | + | As discussed above, the Hohmann transfer involves a trajectory carrying the spacecraft precisely 180° around the Sun. This method requires the lowest expenditure of energy, but does come with the disadvantages of extended travel time and launch window limitations. These disadvantages can be compensated for to a certain degree by increasing fuel expenditure and altering the time of departure. The resultant trajectories will arrive at the target after proceeding less than 180° around the Sun (Type-I Trajectory) or more than 180° (Type-II).<ref name=":1" /> Both trajectory types carry the spacecraft beyond the target orbit and therefore cross it two times—by timing the arrival of the target with one of these two intersections, the spacecraft can still reach its destination, allowing more flexibility in terms of launch times and/or transit duration. These advantages come at the cost of increased energy expenditure: not only does the spacecraft have to accelerate more at the departure point, it also must spend extra fuel decelerating at the destination in order to match the target orbit<ref name=":2" /><ref name=":4" />. For a trip from Earth to Mars, decreasing travel time by 10% necessitates twice as much fuel, while cutting travel time in half requires ten times as much; although these diminishing returns seem undesirable from an efficiency standpoint, they may prove worthwhile when considering factors such as decreased exposure time to radiation for crewed missions or the possibility of arriving in time for a return launch window which the Hohmann transfer would otherwise miss.<ref name=":4" /> |
===Low-thrust relative transfer=== | ===Low-thrust relative transfer=== | ||
| Line 35: | Line 35: | ||
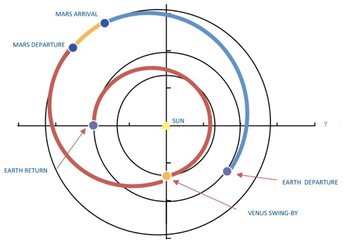
[[File:venusflyby.png|350px|left|thumb|Proposed Mars-return mission demonstrating a modified Hohmann/Type-I Trajectory en route to Mars (blue line) followed by a Venus-assisted flyby upon return.]] | [[File:venusflyby.png|350px|left|thumb|Proposed Mars-return mission demonstrating a modified Hohmann/Type-I Trajectory en route to Mars (blue line) followed by a Venus-assisted flyby upon return.]] | ||
===Gravity assist=== | ===Gravity assist=== | ||
| − | A planet or other astronomical object can accelerate or redirect the trajectory of a passing spacecraft without the use of additional propellant. Probes including Voyager 1 and 2, Galileo, and Cassini have all utilized gravity assists from various planets in order to boost or alter their trajectories without increasing the amount of propellant required.<ref>Basics of Space Flight - Solar System Exploration: NASA Science. (n.d.). Retrieved July 5, 2019, from NASA Solar System Exploration website: <nowiki>https://solarsystem.nasa.gov/basics/chapter4-1/</nowiki></ref> Mission architecture including a flyby of Venus to return a manned crew from Mars to Earth offers the potential for a return launch window which would reduce total mission time (departure, stay on Mars, and return) by roughly 30%, but much of this time would be spent in the return transit near the Sun where spacecraft suffer increased exposure to solar heating.<ref name=":5" /> | + | A planet or other astronomical object can accelerate or redirect the trajectory of a passing spacecraft without the use of additional propellant. Probes including Voyager 1 and 2, Galileo, and Cassini have all utilized gravity assists from various planets in order to boost or alter their trajectories without increasing the amount of propellant required.<ref>Basics of Space Flight - Solar System Exploration: NASA Science. (n.d.). Retrieved July 5, 2019, from NASA Solar System Exploration website: <nowiki>https://solarsystem.nasa.gov/basics/chapter4-1/</nowiki></ref> Mission architecture including a flyby of Venus to return a manned crew from Mars to Earth offers the potential for a return launch window which would reduce total mission time (i.e. departure, stay on Mars, and return) by roughly 30%, but much of this time would be spent in the return transit near the Sun where spacecraft suffer increased exposure to solar heating.<ref name=":5" /> |
| − | |||
| − | |||
| − | |||
| − | |||
| Line 49: | Line 45: | ||
==See also== | ==See also== | ||
| + | |||
*[[Earth-Mars Transfer Trajectory]] | *[[Earth-Mars Transfer Trajectory]] | ||
==References== | ==References== | ||
<references /> | <references /> | ||
Revision as of 10:28, 8 July 2019
volunteer for The Mars Society
It is licensed under Creative Commons BY-SA 3.0 and may be freely shared, but must include this attribution.
In orbital mechanics, a Hohmann transfer describes the path taken to transit between two orbits of differing radii while traveling 180° around their common focus. Conventional analyses consider such a path to be the most efficient transfer method for traveling between circular orbits located on the same plane.[1][2][3]
Contents
Description
Named for Walter Hohmann, the German scientist who first proposed the transfer method in 1925,[4] the Hohmann transfer consists of one half of an elliptical trajectory which connects two concentric orbits. Consider, for example, traveling from one planet (e.g. Earth) to another which is located farther away from the Sun (e.g. Mars). Applying the rules of land-based transit, one might assume that the most efficient way to travel between planets would be to wait until Earth and Mars were as close to one another as their orbits allow and then fly straight towards the target. However, both planets revolve around the Sun at tens of thousands of miles per hour[5] and travel is far from instantaneous over such a vast distance (even at their theoretically closest point, an expanse of 33.9 million miles still separates Earth from Mars[6]).
For this reason, spacecraft must target where Mars will be at the time of arrival, not where Mars is at the time of launch. By targeting an arrival location in Mars’ orbit 180° around the Sun from the launch position at Earth’s orbit, the spacecraft makes maximal use of the Earth’s orbital speed in allowing Mars to catch up to the spacecraft’s location. Just enough propellant is used to reach Mars’ orbit at the intercept location—any less and the spacecraft would fall short, with its elliptical trajectory carrying it back toward its departure point. The final Hohmann trajectory therefore intersects with the Earth’s orbit when closest to the Sun (launch), and with Mars’ orbit when at its farthest point from the Sun (arrival).[1][2]
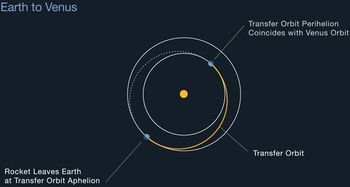
The same principles apply in reverse for travel from a higher orbit to a lower one, such as would be the case in a return trip from Mars or one from Earth to Venus.[2] Again, the idea is to use the minimal energy necessary to reach the desired orbit, traveling 180° around the Sun to arrive at the same time as the target.
Because the Hohmann transfer relies on precise timing and positioning of the trajectory, a mission must wait for the two planets to reach the proper alignment before launching. Departing too soon or too late will still result in the spacecraft passing through the destination orbit, but the target itself will not be present for rendezvous upon arrival.
In the case of an Earth-Mars mission, these opportunities occur only once every 25-26 months[2][7], adding considerable pressure to launch timelines: if a spacecraft finds itself unprepared for launch during the appropriate window, it will have to wait two years for another chance. Furthermore, a separate set of launch windows exist in the reverse direction, so a mission wishing to return to Earth from Mars using a Hohmann transfer in both directions must be capable of sustaining itself on the red planet for roughly 1.5 Earth years before an opportunity to return home becomes available.[8] Accommodating for this extended stay in manned missions constitutes a central feature of Robert Zubrin’s Mars Direct plan.[9]
Alternatives to the Hohmann transfer
Despite the Hohmann transfer’s chief advantage of energy efficiency, other methods exist for traveling between orbiting bodies, with corresponding trade-offs between travel duration and efficiency.
Type-I and Type-II Trajectories

As discussed above, the Hohmann transfer involves a trajectory carrying the spacecraft precisely 180° around the Sun. This method requires the lowest expenditure of energy, but does come with the disadvantages of extended travel time and launch window limitations. These disadvantages can be compensated for to a certain degree by increasing fuel expenditure and altering the time of departure. The resultant trajectories will arrive at the target after proceeding less than 180° around the Sun (Type-I Trajectory) or more than 180° (Type-II).[2] Both trajectory types carry the spacecraft beyond the target orbit and therefore cross it two times—by timing the arrival of the target with one of these two intersections, the spacecraft can still reach its destination, allowing more flexibility in terms of launch times and/or transit duration. These advantages come at the cost of increased energy expenditure: not only does the spacecraft have to accelerate more at the departure point, it also must spend extra fuel decelerating at the destination in order to match the target orbit[3][8]. For a trip from Earth to Mars, decreasing travel time by 10% necessitates twice as much fuel, while cutting travel time in half requires ten times as much; although these diminishing returns seem undesirable from an efficiency standpoint, they may prove worthwhile when considering factors such as decreased exposure time to radiation for crewed missions or the possibility of arriving in time for a return launch window which the Hohmann transfer would otherwise miss.[8]
Low-thrust relative transfer
The Hohmann transfer is known as a two-impulse transfer because it consists of two primary bursts of propulsion: once in the departure orbit to set the spacecraft on its way, and once at the destination to match orbits with the target; the remainder of the transit time is primarily spent coasting, apart from occasional corrective maneuvers.[2][10] This system has its basis in chemical rocket propellants which offer powerful thrust over short periods of time. On the other hand, alternatives such as the ion electric propulsion used by Deep Space 1 offer an efficient way to apply a low level of thrust continuously over longer periods of time.[2] Rather than achieving the desired orbit with short bursts at the beginning and end of the transfer, low-thrust engines gradually enlarge the orbit over time, a process which can be more efficient than the two-impulse Hohmann transfer.[4]
Three-impulse maneuver
When traveling exceptionally long distances between orbits (specifically, when the radius of the outer orbit is over 12 times greater than the inner one), a three-impulse maneuver proves more efficient than the Hohmann transfer.[10] This maneuver involves 1) expanding ones orbit beyond that of the target, 2) creating a second elliptical orbit which matches the target orbit, 3) decelerating in order to match the final target orbit. Although such a maneuver has limited applications in comparison to the Hohmann transfer due to the required ratio of distances as well as the much longer travel time, it does offer efficiency increases given the proper parameters.[10]
Gravity assist
A planet or other astronomical object can accelerate or redirect the trajectory of a passing spacecraft without the use of additional propellant. Probes including Voyager 1 and 2, Galileo, and Cassini have all utilized gravity assists from various planets in order to boost or alter their trajectories without increasing the amount of propellant required.[11] Mission architecture including a flyby of Venus to return a manned crew from Mars to Earth offers the potential for a return launch window which would reduce total mission time (i.e. departure, stay on Mars, and return) by roughly 30%, but much of this time would be spent in the return transit near the Sun where spacecraft suffer increased exposure to solar heating.[9]
Ballistic capture
Rather than targeting a specific rendezvous location as occurs with the Hohmann transfer, the concept of ballistic capture, or low-energy transfer, involves placing the spacecraft ahead of the target in a similar orbit and slightly slower speed, then waiting for the target to catch up and draw the spacecraft into its gravitational field.[12] This proposal reduces the precision needed when syncing a spacecraft's orbit with the target as done in the Hohmann transfer, as well as the fuel required for the mission—for an Earth-Mars transit, fuel savings can reach 25% over the traditional Hohmann transfer.[12] Furthermore, because the spacecraft does not need to arrive at the planet itself, but only in its orbit, launch windows are much more prevalent. On the other hand, such an approach increases travel time by several months, making the method more appropriate for delivering supplies than crews.
Interplanetary Transit Network
This method utilizes Lagrange points, empty space where the gravity between nearby objects balances out such that a body can remain “parked”. Given sufficient time, a spacecraft could transition between these points and different areas of the Solar System at virtually no energy cost—the collection of these pathways is called the Interplanetary Transport Network.[13] Unfortunately, the time involved in such transfers—on the order of generations—renders them of little practical use: a journey from Earth to Mars would take thousands of years.[14]
See also
References
- ↑ 1.0 1.1 Let’s Go to Mars! Calculating Launch Windows Activity. (n.d.). Retrieved July 5, 2019, from NASA/JPL Edu website: https://www.jpl.nasa.gov/edu/teach/activity/lets-go-to-mars-calculating-launch-windows/
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 [2] Basics of Space Flight - Solar System Exploration: NASA Science. (n.d.). Retrieved July 5, 2019, from NASA Solar System Exploration website: https://solarsystem.nasa.gov/basics/chapter4-1/
- ↑ 3.0 3.1 Hohmann Transfer Orbit & Total Travel Time. (2001). Retrieved July 5, 2019, from http://www.polaris.iastate.edu/EveningStar/Unit6/unit6_sub2.htm
- ↑ 4.0 4.1 [4] Hohmann transfer orbit. (2019). In Wikipedia. Retrieved from https://en.wikipedia.org/w/index.php?title=Hohmann_transfer_orbit&oldid=897743154
- ↑ Rocheleau, J. (2013, October 15). Orbital Speed of Planets in Order - Rotational Speed Comparison. Retrieved July 5, 2019, from Planet Facts website: http://planetfacts.org/orbital-speed-of-planets-in-order/
- ↑ Sharp, T. (2017, December 15). How Far Away is Mars? | Distance to Mars. Retrieved July 5, 2019, from Space.com website: https://www.space.com/16875-how-far-away-is-mars.html
- ↑ Kayton, M. (n.d.). Hohmann transfer orbit diagram. Retrieved July 5, 2019, from http://www.planetary.org/multimedia/space-images/charts/hohmann-transfer-orbit.html
- ↑ 8.0 8.1 8.2 8.3 How long is the trip? (n.d.). Retrieved July 5, 2019, from http://www.polaris.iastate.edu/EveningStar/Unit7/unit7_sub3.htm
- ↑ 9.0 9.1 Zubrin, R. (2011). The Case for Mars. Simon & Schuster.
- ↑ 10.0 10.1 10.2 Widnall, S., & Peraire, J. (2008). Orbit Transfers and Interplanetary Trajectories. 12.
- ↑ Basics of Space Flight - Solar System Exploration: NASA Science. (n.d.). Retrieved July 5, 2019, from NASA Solar System Exploration website: https://solarsystem.nasa.gov/basics/chapter4-1/
- ↑ 12.0 12.1 Hadhazy, A. (2014, December 22). A New Way to Reach Mars Safely, Anytime and on the Cheap. Retrieved July 5, 2019, from Scientific American website: https://www.scientificamerican.com/article/a-new-way-to-reach-mars-safely-anytime-and-on-the-cheap/
- ↑ Cain, F. (2016, November 15). What Is The Interplanetary Transport Network? Retrieved July 5, 2019, from Universe Today website: https://www.universetoday.com/131953/interplanetary-transport-network/
- ↑ Interplanetary Transport Network. (2019). In Wikipedia. Retrieved from https://en.wikipedia.org/w/index.php?title=Interplanetary_Transport_Network&oldid=889884788