Lagrangian point
Contents
- 1 Definition
- 2 Positions of the Lagrangian points
- 3 Current missions using the Lagrangian points of the Earth-Sun system
- 4 Objects observed in the Mars-Sun Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_4} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_5} points
- 5 Uses of the Mars Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2} points
- 6 See also
Definition
A Lagrangian point is a point of interplanetary gravitational stability in a two body orbital configuration. Devised by the Italian/French mathematician and astronomer, Joseph Louis Lagrange (1736-1813), Lagrangian points are currently used to describe the influence of the planets over local space, provides a location for Trojan asteroids and may possibly be used by future space missions as a "stepping stone" to Mars and the Moon.
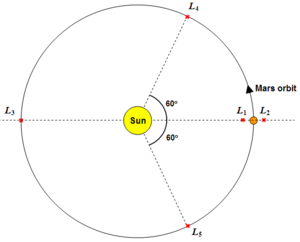
Positions of the Lagrangian points
The simplest Lagrangian point to understand is the "first Lagrangian" (or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1} ) point between the Earth and the Sun. The point at which the gravitational pull of the Sun and the gravitational pull of the Earth cancels out (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{Earth}+g_{Sun}=0} ) creates an island of gravitational stability where space observatories, or indeed space stations, can be positioned.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2} is located on the opposite side of the smallest orbital body (in this case, the Earth) to . This very stable region is also useful to space observatories observing the cosmos. The Earth in this case will be constantly eclipsing the Sun, allowing sensitive optics to operate free of noise emitted from the Sun.
is a less-stable Lagrangian point on the far side of the Sun. In this case, the Earth's gravitational force is negligible, allowing other planet's orbits to interfere with the gravitational stability of the region.
and are points leading and trailing the orbiting body at an angle of approximately 60° from the Earth-Sun line. These points are also known as "Trojan points" where asteroids (known as Trojan asteroids) become captured by the relative gravitational stability and orbit with the orbital body.
Calculating the position of and
If the mass of the larger body is massively greater than that of the orbiting body (as is the case in the Earth, or Mars, around the larger Sun), the following equation[1] can be applied:
where is the distance of or from the orbiting body, is the distance between the bodies and and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_1} are the masses of the smaller and larger bodies respectively.
Current missions using the Lagrangian points of the Earth-Sun system
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1}
- The Solar and Heliospheric Observatory (SoHO) - A multi-instrument observatory contantly observing the Sun.
- Advanced Composition Explorer (ACE) - An in-situ observatory measuring the properties of the solar wind and solar radiation.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2}
- Wilkinson Microwave Anisotropy Probe (WMAP) - Surveying the sky, observing the microwave radiation left over by the Big Bang.
Objects observed in the Mars-Sun Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_4} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_5} points
Asteroids in the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_4} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_5} Mars-Sun Lagrangian points are often called Mars Trojan asteroids. A handful of asteroids are in stable solar orbits, leading (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_4} ) and following (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_5} ) the path of Mars including an asteroid named "1999 UJ7" (at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_4} ) and "5261 Eureka" (at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_5} ).
Uses of the Mars Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_2} points
- An "early warning system" to notify settlers about the onset of solar storms.
- Communications satellites inserted in stable orbits around the Lagrangian points - long-term nodes of communication between Earth and Mars. Could be extended to include the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_4} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_5} points to allow communication even when Mars is in conjunction.
- A manned space station acting as a "staging post" for missions to asteroids or refuge before making the final plunge into Mars' gravitational well.





![{\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1175643479ba922598c78a6d4dfcf7fff160bfe7)









