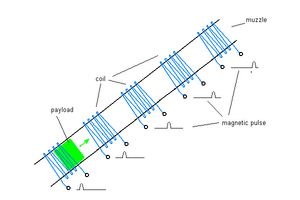
Mass driver
The transport from the surface of Mars to Mars' orbit and vice versa can be achieved by a mass driver or electromagnetic catapult. The idea is to install an electrical linear motor on the surface, pointing towards the desired orbit in an appropriate angle. Either a orbital catcher system or a smart payload are required to put the payload into orbit. Otherwise the payload follows either an elliptical orbit back to the surface and is lost, or must exit Mars' influence at faster than the escape velocity.
A mass driver is powered electrical and requires no chemical fuels if a catcher is available, or chemical motors on the payload. While on Earth this would not work for lifting people to orbit, the conditions of Mars might allow it. The acceleration of persons is limited to a few g, so the linear motor must be very long for that case.
Sky ramps are very similar, but they use rockets rather than a mass driver, and only act as a reusable first stage rather than launching a ship directly into orbit.
Contents
Launching a payload
The payload is accelerated along the linear motor until it reaches the end of the linear motor and gains enough velocity to get to the desired orbit just by inertia. The velocity must be higher than the escape velocity because of the braking effect of the Martian atmosphere. (needs equation and air resistance calculation)
Mars' escape velocity is 5,020 m/s. If you accelerated at 6 gravities, then this would take ~86 seconds to reach orbital velocity. This would require a mass driver which would be 218 km long. (This distance is about 1/3 of the of the width of Olympus Mons. If you wished to use a smaller volcano, then a higher acceleration would be needed.)
The payload would need to have small rockets to circularize the orbit, or be captured by an orbital catcher.
Note, that reaching orbital velocity requires a very large and powerful mass driver. But if you wanted to reach (say) ONE HALF orbital velocity, the engineering of the mass driver is much easier and less expensive. A mass driver which thus helps a rocket, would allow single stage to orbit rockets with marvellous mass ratios. So smaller and cheaper mass drivers could be useful for a developing colony.
Catching a payload
A mass driver cannot launch a payload directly into orbit due to orbital mechanics. A force must be exerted on the payload to circularize the orbit, either with a catcher or chemical propulsion. If chemical propulsion is chosen, then the payload becomes a form of rocket, and for economical operation must be returned to the surface and re-used, and the end result is a form of hybrid with the Sky ramp. If a catcher is used, the catcher can in turn use a mass driver or electrical propulsion via SEP on NEP to transfer energy to the captured payload. The catcher loses some energy by transfer to the payload that must be restored by propulsion, although it might be possible to use excess velocity from the payload as energy transfer, with the risk of losing the payload if timing is not perfect. With proper coordination the catcher can be reached by the mass with the same velocity (although not the same vector).
Landing a payload
Just like launching, the landing of a payload can be done. The trajectory of the payload from outer space or from an orbit to the muzzle of the mass driver must be adjusted with nearly perfect accuracy. When entering the muzzle, the payload has a very high velocity, nearly as high as the escape velocity. The payload is decelerated by the linear motor until it comes to a halt. However, again du to orbital mechanics, the launcher outlet cannot be the landing inlet and two mass drivers are required, increasing capital costs significantly.
If adequate energy storage facilities are added to the system, and if a sufficiently massive product is required on Mars, the system could be net 0 energy, with the exception of aerodynamic losses.
Possible locations
Since the viability of a mass driver increases with a lowered atmospheric pressure, the location of the mass driver's muzzle should be as high as possible. The top (or rim) of Olympus Mons (the highest mountain in the solar system) might be a good choice. It is about 625 km wide and 25 km tall. It has an air pressure of about 40 Pa at top.[1][2] (Note that 40 Pa = 0.0004 bar, so this is a high grade vacuum.)
Olympus Mons also offers a natural ramp. The mass driver must be almost perfectly straight (there is a slight curve for Coriolis forces caused by the rotation of the planet while launching) so tunnels, cuts and bridges will have to be made.
Pavonus Mons is a tall volcano directly on the Equator which could be suitable if equatorial launches are preferred. It is 375 km wide and 14 km high, so an acceleration of 9 gees for 57 seconds would require a mass driver 143 km long.
Open issues
- How strong is the effect of air friction at an altitude of the Olympus Mons top? Does it have a damaging effect on a steel hull? This is mach 14.5 which is about 1/5 of the atmospheric heating caused by reentry on Earth IF the air pressure was equal. However, maximum heating in Earth reentry is at about 100km attitude, and 40 Pa is 1/4 this. So steel should be able to handle this amount of heating, especially since it would rapidly decrease as the ship went higher. The friction WOULD be enough that the minimum speed of 5,020 m/s would not reach orbit. Either the mass driver must give extra speed to make up for friction, or the payload would want a small rocket to over come the velocity lost, and to circularize the orbit once high enough.
- Normal people can withstand 9 gravities (gees) of acceleration for about 1 minute. 6 gees of acceleration can be withstood for around 10 minutes.
references
- ↑ Public Access to Standard Temperature-Pressure Profiles Standard Pressure Profiles measured by MGS Radio Science team at 27 km range from approx 30 to 50 pascals
- ↑ Late Martian Weather! stanford.edu temperature/pressure profiles 1998 to 2005