Lagrangian point
Contents
Definition
A Lagrangian point is a point of interplanetary gravitational stability in a two body orbital configuration.
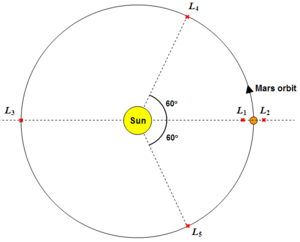
Positions of the Lagrangian points
The simplest Lagrangian point to understand is the "first Lagrangian" (or ) point between the Earth and the Sun. The point at which the gravitational pull of the Sun and the gravitational pull of the Earth cancels out () creates an island of gravitational stability where space observatories, or indeed space stations, can be positioned.
is located on the opposite side of the smallest orbital body (in this case, the Earth) to . This very stable region is also useful to space observatories observing the cosmos. The Earth in this case will be constantly eclipsing the Sun, allowing sensitive optics to operate free of noise emitted from the Sun.
is a less-stable Lagrangian point on the far side of the Sun. In this case, the Earth's gravitational force is negligable, allowing other planet's orbits to interfere with the gravitational stability of the region.
and are points leading and trailing the orbiting body at an angle of approximately 60° from the Earth-Sun line. These points are also known as "Trojan points" where asteroids (known as Trojan asteriods) become captured by the relative gravitational stability and orbit with the orbital body.